画画为什么要学习透视？

一个学画画不久的人，往往会从实践中得到一些有关的透视知识如：近大远小，一个正方形的桌面到了画中要画成斜方形，正圆的杯口在画中要画成椭圆形等。但只是这一点初步的感性认识是很不够的，我们所要表现的物体是如此之多，形象是如此复杂，空间又是如此之大，只凭“近太远小”这样的口诀是不能彻底解决透视中的所有问题。近者要大到什么程度？远要小到什么程度？正方形要画成斜方形，究竟如何斜法才算正确？

深入仔细地分析思考起来就不那么简单，就是绘画技巧比较熟练的画家，若不细心对待往往也会出现一些透视上的错误，特别是写生和创作构图更需要透视理论的指导，因为它关系到作者设想中人与人、人与物、人与景等方面的问题，如果不掌握科学的技法理论知识则不利于体现作品的主题思想，对画面的主次、空间、远近、虚实等关系就不容易处理好，从而失去了画面的艺术性、完整性。因此必须理性地根据科学的法则来研究透视的变化规律，使我们能在平面的画纸上准确地表现出富有立体感、空间感、生动感的艺术作品。

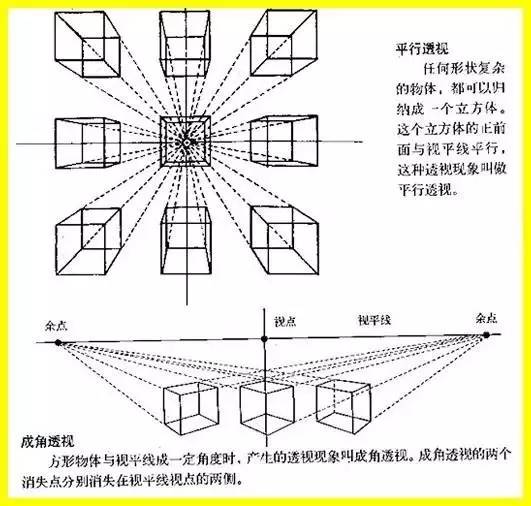
怎样理解透视学在绘画中的应用？

透视有三种：1、色彩透视；2、消逝透视；3、线透视。 这是达芬奇总结的，其中最常用到的是线透视。透视学在绘画中占很大的比重，它的基本原理是在画者和被画物体之间假想一面玻璃，固定住眼睛的位置（用一只眼睛看），连接物体的关键点与眼睛形成视线，再相交与假想的玻璃。在玻璃上呈现的各个点的位置就是你要画的三维物体在二维平面上的点的位置，这是西方古典绘画透视学的应用方法。

1、视点—→ 你眼睛所在的地方。

2、视线—→ 视点与物体任何部位的假象连接。

3、视角—→ 视点与任意两条视线之间的夹角。

4、视域—→ 眼睛所能看到的空间范围。

5、视锥—→ 视点与无数条视线构成的圆锥体。

6、视距—→ 视点到心点的垂直距离。

7、视平线—→ 与人眼等高的一条水平线。

8、视中线—→ 通过新店与视平线成直角的线。

9、消失点—→ 遵循“近大远小”透视原则，实现的无限远的消失点。

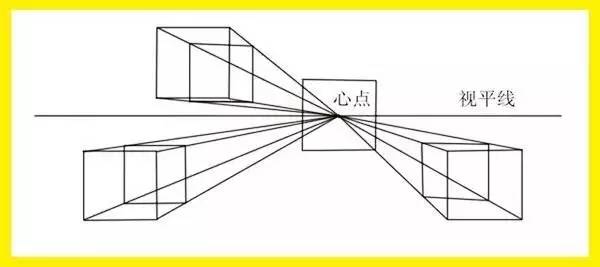
10、心点—→ 视平线与视中线的相交点。

11、天、地点和左、右余点： 视平线上、下、左、右消失的点。

上述两种情况之外的都是三点透视。

★ 面积越来越小，最终消失在左余点上。

★ 越往右，这个立方体就越小越上，最终消失在右余点上。

★ 越往下，越来越小，最终消失在地点上。

立方体的透视关系

想画好立方体，小伙伴需要要掌握以下两点：

⑴透视

⑵形体塑造（塑造只要是依赖于明暗变化的规律）

小伙伴掌握好这两点，正方体就算学明白了。以后再画长方体、多面体以及其他复杂的形体就是相当容易滴！

透视从大的方向来理解，无非就是近大远小的原理了。可是这个原理却有许多小伙伴没有理解全面的哦。当我们面对较小的物体可能会出现的三种透视：无透视、两点透视、三点透视。是小伙伴最常见的，也是小伙伴必须要掌握的。

接下来和小编一起分析下图的三个透视面：

圆柱体的透视关系

圆柱体的两个面-----一个立面一个平面，之前讲正方体透视时说过看见两个面就是两点透视。

以圆柱体为例，小编要说的是：小伙伴在画顶部圆的时候，可以以长方形代替下图左上方的梯形，但近大远小是务必要注意的。同时，圆柱体底端的圆宽度上要略短于上方的圆，而长度上略长于上方的圆；其顶端的圆的边线弧度也要比底端的圆的弧度要缓些。因为透视的作用，下图圆柱体的两个圆平面都是后半弧扁平。

透视不仅可以使物体看起来多维、饱满，还可以用来制造聚拢感、距离感和空间感。

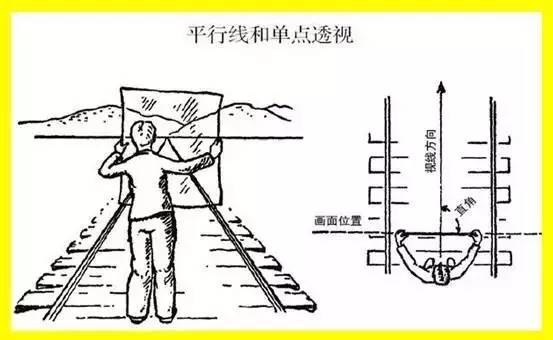
让我们随着火车铁轨走到平原，在那儿能看到一望无垠的平整的土地。遥望四周，远处绵延的土地与天相接连成一条直线。

这条线就是“地平线”

▼

解说地平线最好的例子就是眺望一大片空旷的水体，目之所及，只有水面，看不见海岸。在大海上，地平线就是一条无限延伸的线。

尽管我们的视线总是受到各种物体的干扰，比如一只手，一幢大楼，一座高山，我们把地平线理解为无限延伸的。即便我们走进一幢大楼，关了门，地平线依旧不声不响地存在着。

如果遮掩地平线的所有物体都是透明的，那么地平线将毫无阻拦地一直出现在人们的视线里。对此详见下页图示。

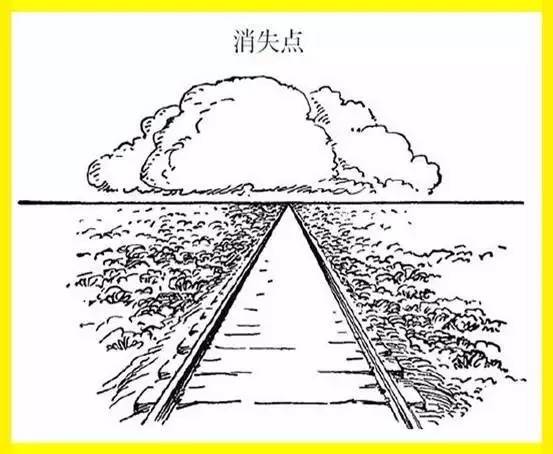
现在，我们站在两条锃光发亮的铁轨中间，铁轨在平原上一直延伸下去，直到在远方接触地平线的那一刻便从我们的视野里消失了。

我们把铁轨消失的地方称为“消失点”

▼

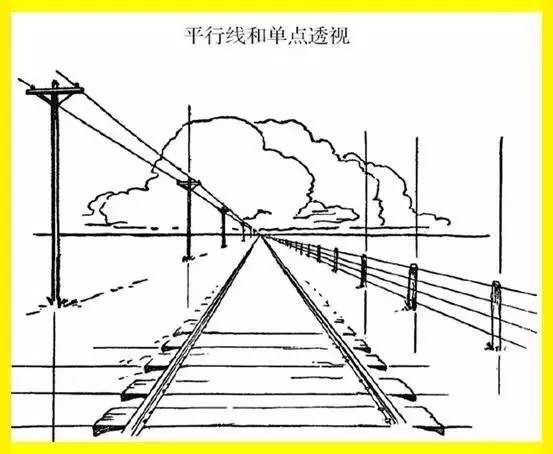
第一张玻璃纸或一块玻璃与身体平行，且与地面垂直。透过透明的玻璃，你能看到前方的景物和物体。若要把所见物体落实到这张玻璃纸上，就需要用到透视法。我们可以把这张玻璃纸看做画纸或油画的帆布。如上图所示放置时，我们称其为“画面”。透视就是在画面上完成的。“画面”垂直于地面，处于画家和所画物象之间，且如下图右所示，画面与视线方向成直角。

两个消失点

（两点透视）

高线

▼

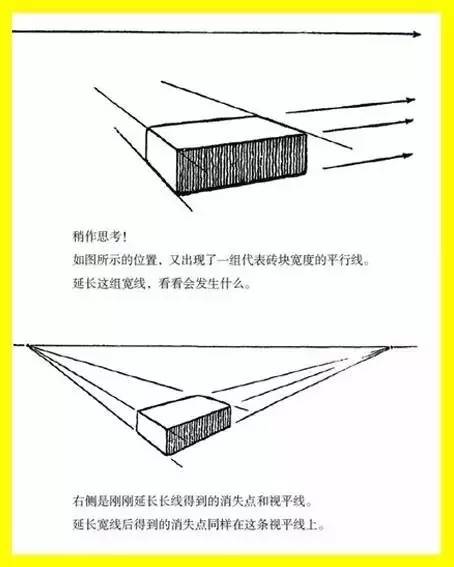
当消失点位处砖块中心的正上方，我们又得到一幅铁轨透视的模型图：一组相交的平行线（铁轨）和一组平行于地平线的平行线（枕木）。第二组平行线也可以理解为其平行于画面。

三组平行线

定位消失点和视平线

▼

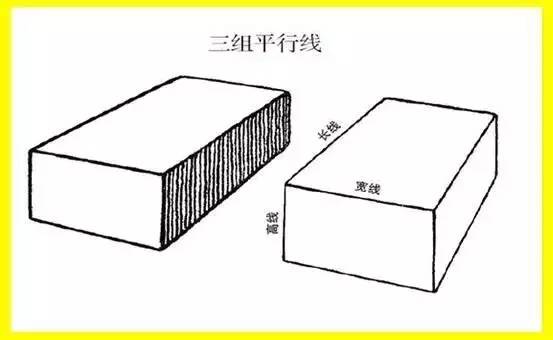
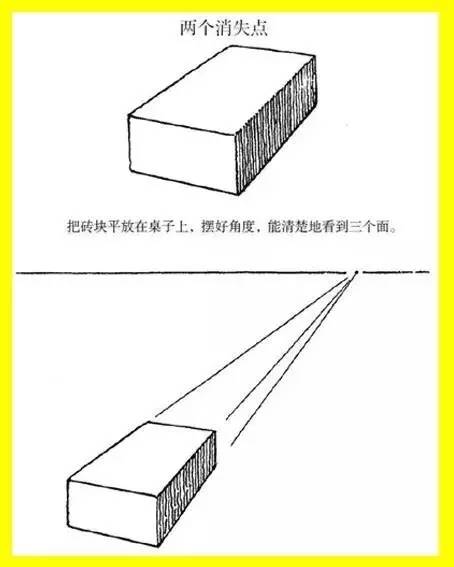
上图左是一块普通砖块。

长方体本有六面，但在画面中只能看到三个面。上图右标示出来的直线即每两面相交后所得相交线。如果把六个面每两面的交线都画出来，那就是12条线。

4条长线，即砖块的长度，是平行的。

4条宽线，即砖块的宽度，是平行的。

4条高线，即砖块的高度（或者说厚度），也是平行的。

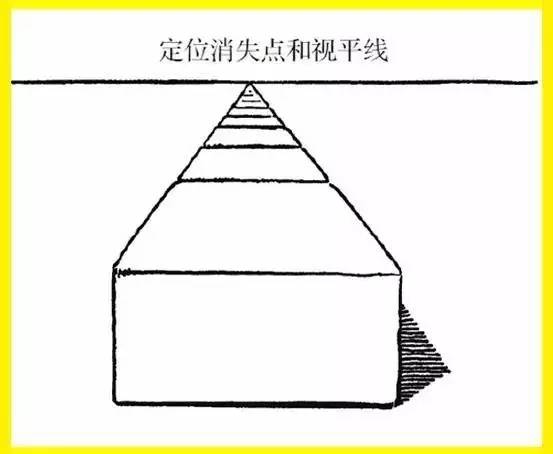
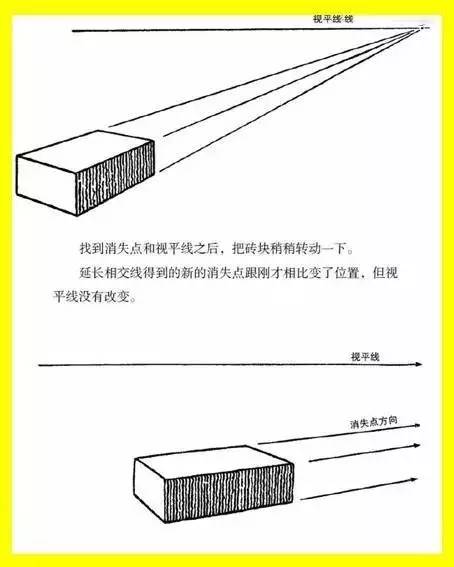
还记得小时候把砖块一块接一块地连起来当做铁轨吗？现在让我们再试一次。你会发现我们在前几章节讨论过的平原上的铁轨的特征——视平线、消失点等对这一排砖块同样适用。现在我们拿掉其他砖块，只留下一块。

只要延伸两侧直线直至相交，我们便能再一次定位消失点和视平线。两条延长线的交点即消失点。穿过消失点的水平直线即视平线。因此，在透视时，只要延伸任意两条代表平行关系的平行线，我们就可以找到消失点和视平线。

透视的几个重点

1.近大远小。两个体积相同的物体一个在你眼前一个在100米外，是不是近处的看上去大呢?

2.近宽远窄。例如下图的立方体透视图近处的那个边就比远处的边宽。还有你站在铁路中间往远处看是不是铁路会越来越窄。

3.近实远虚。距离你近的物体相信你会看到更清晰，远处的就比较模糊。